Астрорасчеты для камер
CCD arc-sec/pixel and focal ratio
arc-sec/pixel using known object size
f/ratio
focal length using known object size
CCD Critical Sampling
Focal reducers
CCD Dust Shadows
CCD Filter Reflections
Signal to noise ratio
Critical Focus Zone & CCD Focus Zone
CCD arc-sec/pixel & Focal Ratio
The formula for arc-sec per pixel is:
Alternatively you can measure the size of an imaged object in pixels, and divide that objects known size in arc-seconds by the size in pixels.
Solving for focal ratio, this becomes:
You can use this formula to get a reasonably accurate focal ratio from any image where you know the angular size of an object (or angular distance between two stars).
Or if you want the focal length used for an image and know the angular size of the object imaged:
![focal length = (object[pix] * pix_size * 206.3) / object[arcsec]](/sites/default/files/calc/formula28.png){kind=small}
CCD Planetary Critical Sampling
Use this formula to calculate the minimum focal length required to fully sample a high resolution image with any particular CCD.
This is based on the assumption of perfect seeing and the Airy disk being the limit of resolution. For planetary imaging using 'lucky' imaging short exposure techniques this is a reasonable assumption. For long exposures the FWHM value for any particular night would be a better measure of the resolution obtainable.
I have made the assumption that adequate sampling requires the pixel spacing to be three times greater than the scopes resolution (forget Nyquist!)
Focal Reducers
Use this formula to calculate the resulting focal ratio when using a focal reducer:
And this one to calculate the amount of in-focus required by that set-up:
Where
a = Distance of CCD from focal reducer
b = Focal length of FR
c = Focal ratio of scopeThe Meade/Celestron focal reducers have the following focal lengths.
[note: Around 2006 Meade manufactured some 0.63 focal reducers with a focal length of around half what they should be making them unsuitable for use with SLR cameras or filter wheels, any marked "Japan" are OK, as are later "China" ones.]:FR 0.33x focal length = 85mm
FR 0.63x focal length = 285mmWilliam Optics 0.8x FR focal length = 260mm
ATIK 0.5x FR focal length = 80mm
* Note that the in-focus figure assumes that the FR-CCD spacing is added to your physical imaging train length (as when using the Meade/Celestron FR's with spacing tubes). If you are using a FR like the ATIK that is fitted internally, then you have to add the FR-CCD spacing to this figure (to make it smaller). If you are using a FR like the Meade/Celestron then you will have to subtract the depth of the FR itself to this figure (to make it a larger negative number).
CCD Dust Shadows
If you are troubled by dust shadows on your CCD images you can calculate the distance that the dust particle is in front of the CCD with the following formula:
Where:
Dist = Distance from CCD surface in mm
p = CCD pixel size in microns
f = Focal ratio of imaging system
d = Diameter of dust shadow in pixels
CCD Filter Reflections
Want to know where those annoying reflection disks around stars are coming from?...
To calculate this
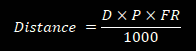
Where:
Dist = Distance from CCD of reflection surface in mm
D = Diameter of reflection disk in image in pixels
P = CCD pixel size in microns
FR = Focal ratio of imaging system
Signal to Noise Ratio
A simplified formula for calculating the signal to noise ratio in an image is:
where:
S = total nebula signal
B = total background signal
D = dark current
RN = read noise from bias frame
n = number of sub-exposures
Critical Focus Zone
Calculate the length of the zone in which the focused image of a star is smaller than the size of its Airy disk.
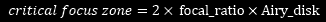
which simplifies to:
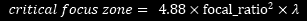
For CCD cameras, if we take a 2x sampling ratio:
where:
λ = wavelength of light
Note that because at low f/ratios the size of the Airy disk becomes significantly smaller than typical CCD pixels sizes I have introduced a value for the CCD Focus Zone. The value for the CCD focus zone takes the larger value of the CFZ, or where the Airy disk is half the effective pixel size (2x under sampling ratio) the CCD focus zone value defined above. For small focal ratios the CFZ gives a misleadingly small figure for imagers.